-
Welcome to your Moodle site
Now, you are in control!
Here are some links of interest:
Skip available coursesAvailable courses
This course covers:
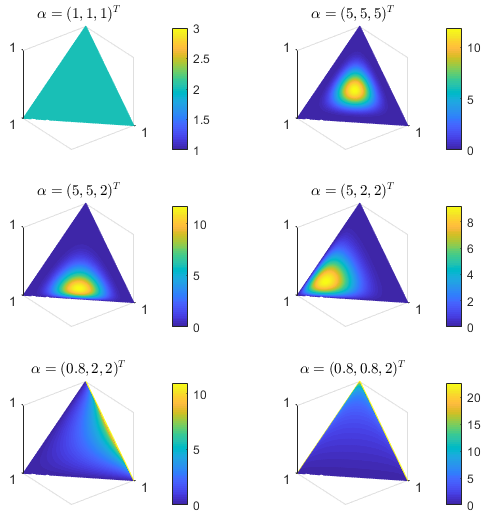
- Independence, Probability Rules and Simpson’s Paradox,
- Probability Densities, Expectation, Variance and Moment,
- Examples of Discrete Probability Mass Functions,
- Examples of Continuous Probability Density Functions,
- Functions of Continuous Random Variables,
- Conjugate Probability Distributions,
- Graphical Representations.
This course covers:
- Inverse Transform Sampling,
- Rejection Sampling,
- Importance Sampling,
- Markov Chains,
- Markov Chain Monte Carlo.
This course covers:
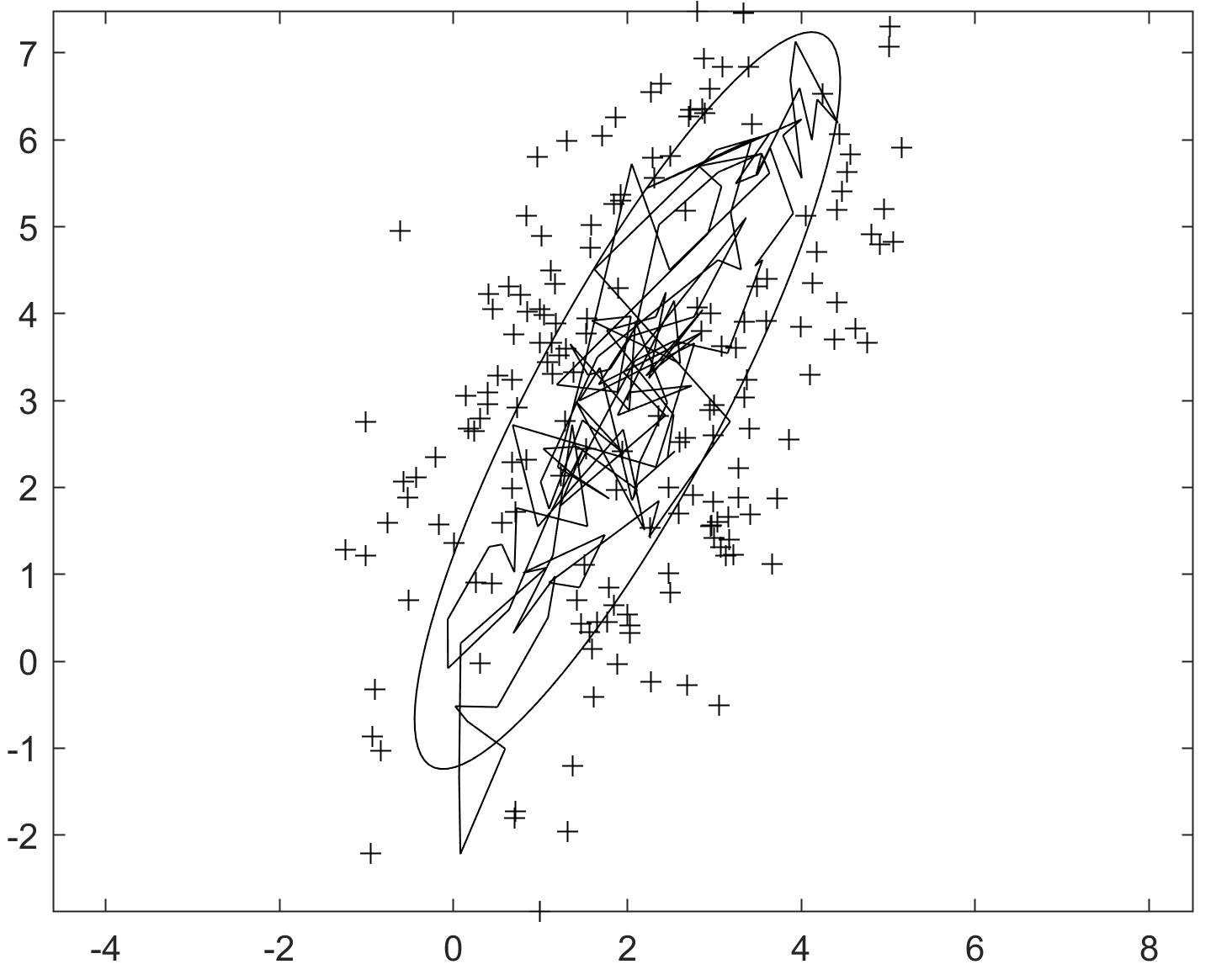
- Features,
- Projections onto Subspaces,
- Fisher’s and Linear Discriminant Analysis,
- Multiple Classes,
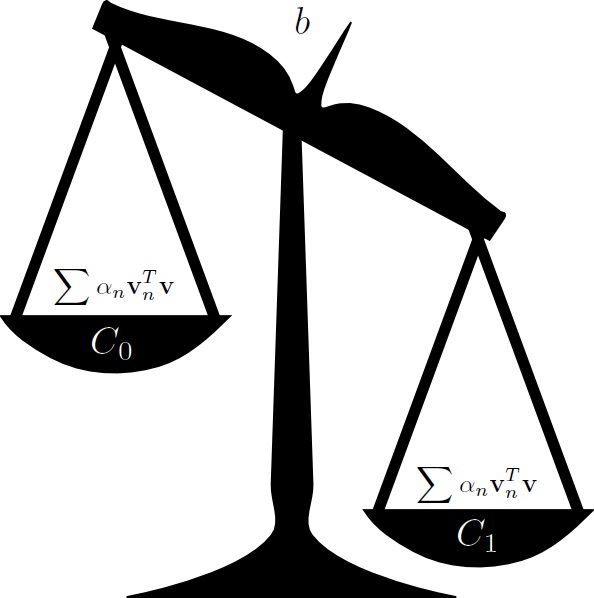
- Online Learning and the Perceptron,
- The Support Vector Machine.
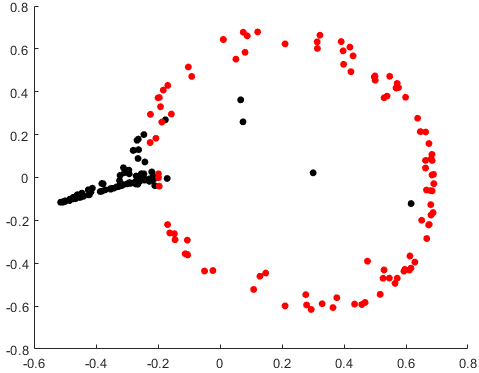
This course covers:
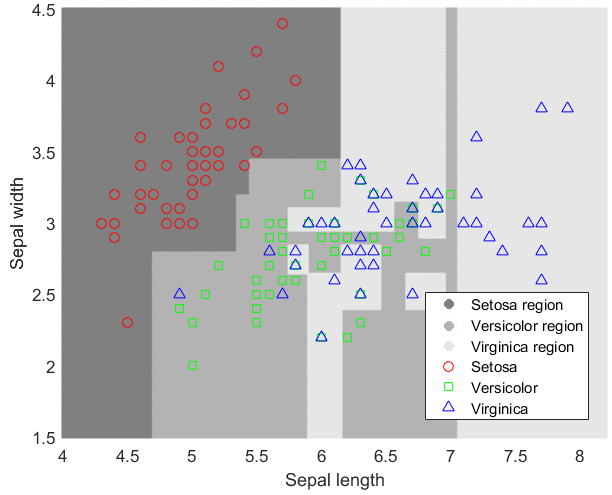
- Quadratic Discriminant Analysis,
- Kernel Trick,
- k Nearest Neighbours 123
- Decision Trees,
- Neural Networks,
- Boosting and Cascades.
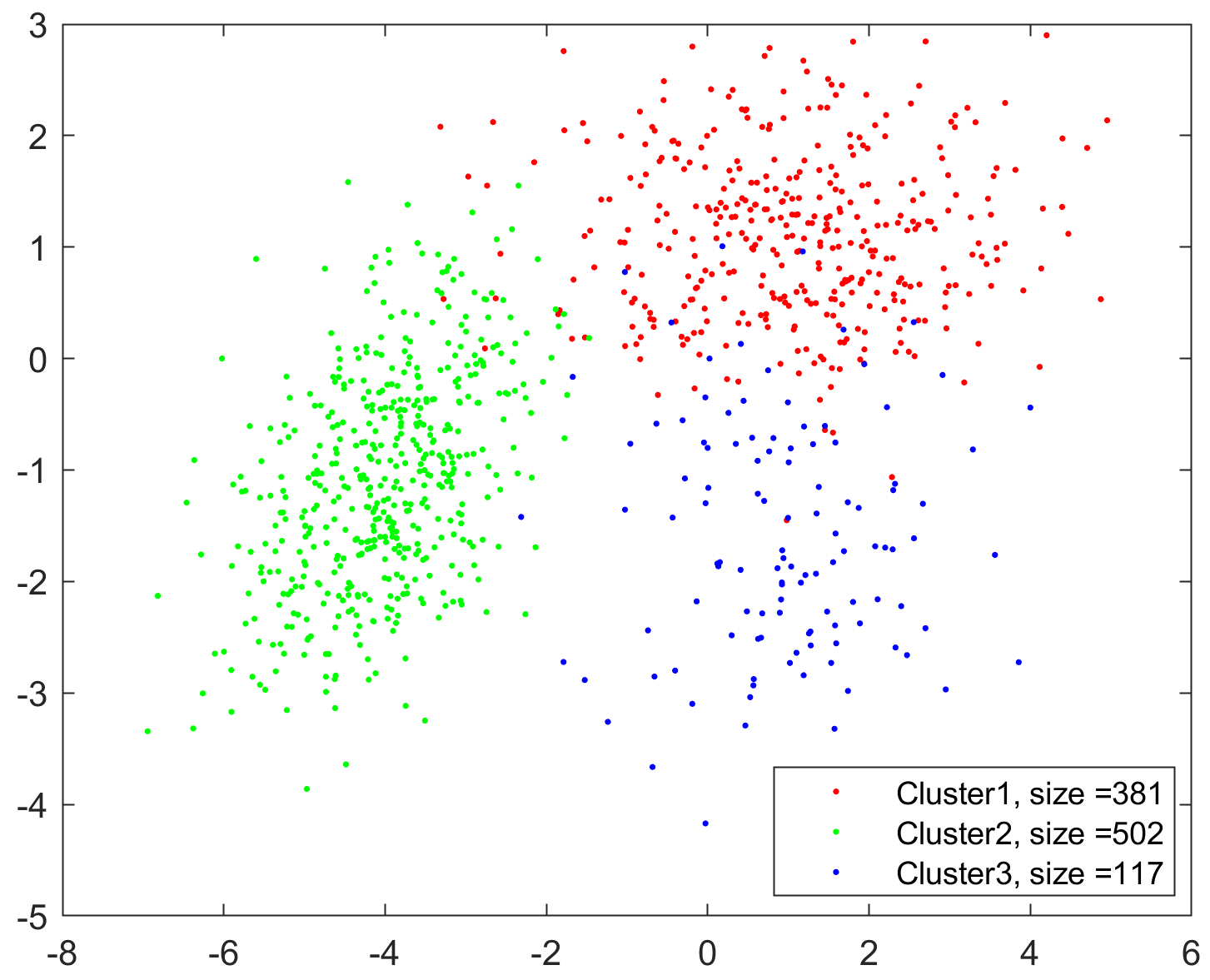
This course covers:
- K Means Clustering,
- Mixture Models,
- Gaussian Mixture Models,
- Expectation-Maximization,
- Bayesian Mixture Models,
- The Chinese Restaurant Process,
- Dirichlet Process.
This course covers:
- Principal Component Analysis,
- Probabilistic View,
- Expectation-Maximization,
- Factor Analysis,
- Kernel Principal Component Analysis.
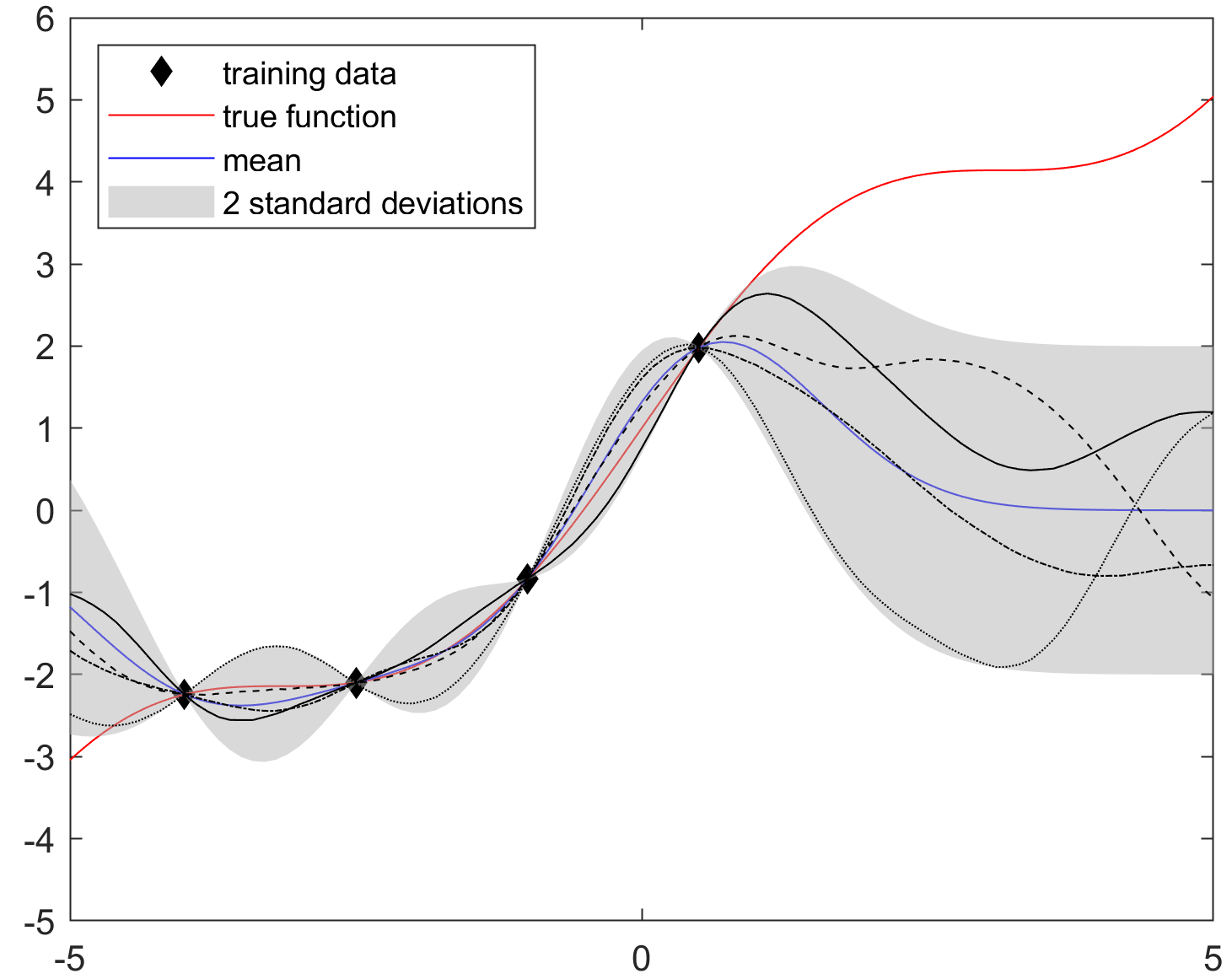
This course covers:
- Problem description,
- Linear Regression,
- Polynomial Regression,
- Ordinary Least Squares,
- Over- and Under-fitting,
- Bias and Variance,
- Cross-validation,
- Multicollinearity and Principal Component Regression,
- Partial Least Squares,
- Regularization,
- Bayesian Regression,
- Expectation–Maximization,
- Bayesian Learning,
- Gaussian Process.
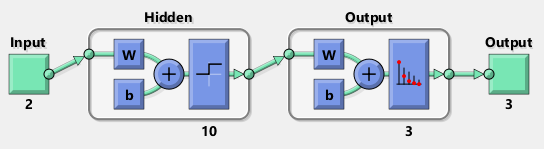
This course covers:
- Neural Networks,
- Error Backpropagation,
- Autoencoders,
- Autoencoder Example,
- Relationship to Other Techniques,
- Indian Buffet Process.
This course covers:
- Floating Point Arithmetic,
- Overflow and Underflow,
- Absolute, Relative Error, Machine Epsilon,
- Forward and Backward Error Analysis,
- Loss of Significance,
- Robustness,
- Error Testing and Order of Convergence,
- Computational Complexity,
- Condition.
This course covers:
- Simultaneous Linear Equations,
- Gaussian Elimination and Pivoting,
- LU Factorization,
- Cholesky Factorization,
- QR Factorization,
- The Gram–Schmidt Algorithm,
- Givens Rotations,
- Householder Reflections,
- Linear Least Squares,
- Singular Value Decomposition,
- Iterative Schemes and Splitting,
- Jacobi and Gauss–Seidel Iterations,
- Relaxation,
- Steepest Descent Method,
- Conjugate Gradients,
- Krylov Subspaces and Pre-Conditioning,
- Eigenvalues and Eigenvectors,
- The Power Method,
- Inverse Iteration,
- Deflation.
This course covers:
- Lagrange Form of Polynomial Interpolation,
- Newton Form of Polynomial Interpolation,
- Polynomial Best Approximations,
- Orthogonal polynomials,
- Least-Squares Polynomial Fitting,
- The Peano Kernel Theorem,
- Splines,
- B-Spline.
This course covers:
- Bisection, Regula Falsi, and Secant Method,
- Newton’s Method,
- Broyden’s Method,
- Householder Methods,
- Muller’s Method,
- Inverse Quadratic Interpolation,
- Fixed Point Iteration Theory,
- Mixed Methods.
This course covers:
- Mid-Point and Trapezium Rule,
- The Peano Kernel Theorem,
- Simpson’s Rule,
- Newton–Cotes Rules,
- Gaussian Quadrature,
- Composite Rules,
- Multi-Dimensional Integration,
- Monte Carlo Methods.
This course covers:
- Finite Differences,
- Differentiation of Incomplete or Inexact Data.
This course covers:
- One-Step Methods,
- Multistep Methods, Order, and Consistency,
- Order Conditions,
- Stiffness and A-Stability,
- Adams Methods,
- Backward Differentiation Formulae,
- The Milne and Zadunaisky Device,
- Rational Methods,
- Runge–Kutta Methods.
This course covers:
- Classification of PDEs,
- Parabolic PDEs,
- Finite Differences,
- Stability and Its Eigenvalue Analysis,
- Cauchy Problems and the Fourier Analysis of Stability,
- Elliptic PDEs,
- Computational Stencils,
- Sparse Algebraic Systems Arising from Computational Stencils,
- Hockney Algorithm,
- Multigrid Methods,
- Parabolic PDEs in Two Dimensions,
- Hyperbolic PDEs,
- Advection Equation,
- The Wave Equation,
- Spectral Methods,
- Spectral Solution to the Poisson Equation,
- Finite Element Method.